EM-like algorithm for the GMCM

An fast and modified implementation of the Li et. al. (2011) EM-like algorithm for estimating the maximizing parameters of the GMCM-likelihood function.

PseudoEMAlgorithm(x, theta, eps = 1e-04, max.ite = 1000,
  verbose = FALSE, trace.theta = FALSE, meta.special.case = FALSE,
  convergence.criterion = c("absGMCM", "GMCM", "GMM", "Li", "absLi"))

Arguments

x	A matrix of observations where rows corresponds to features and columns to experiments.
theta	A list of parameters formatted as described in `rtheta`.
eps	The maximum difference required to achieve convergence.
max.ite	The maximum number of iterations.
verbose	Logical. Set to `TRUE` to increase verbosity.
trace.theta	Logical. If `TRUE`, a trace of the estimated thetas are returned.
meta.special.case	Logical. If `TRUE`, the estimators used are for the special case GMCM of Li et. al. (2011).
convergence.criterion	Character. Sets the convergence criterion. If `"absGMCM"` the absolute value of difference in GMCM is used. If `"GMCM"` the difference in GMCM-likelihoods are used as convergence criterion. If `"GMM"`, the guaranteed non-decreasing difference of GMM-likelihoods are used. If `"Li"`, the convergence criterion used by Li et. al. (2011) is used. If `"absLi"`, the absolute values of the Li et. al. criterion.

Value

A list of 3 or 4 is returned depending on the value of trace.theta

theta

A list containing the final parameter estimate in the format of rtheta

loglik.tr

A matrix with different log-likelihood traces in each row.

kappa

A matrix where the (i,j)'th entry is the probability that x[i, ] belongs to the j'th component. Usually the returned value of EStep.

theta.tr

A list of each obtained parameter estimates in the format of rtheta

Details

When either "absGMCM" or "absLi" are used, the parameters corresponding to the biggest observed likelihood is returned. This is not necessarily the last iteration.

Note

The algorithm is highly sensitive to the starting parameters which therefore should be carefully chosen.

References

Li, Q., Brown, J. B. J. B., Huang, H., & Bickel, P. J. (2011). Measuring reproducibility of high-throughput experiments. The Annals of Applied Statistics, 5(3), 1752-1779. doi:10.1214/11-AOAS466

Author

Anders Ellern Bilgrau <anders.ellern.bilgrau@gmail.com>

Examples

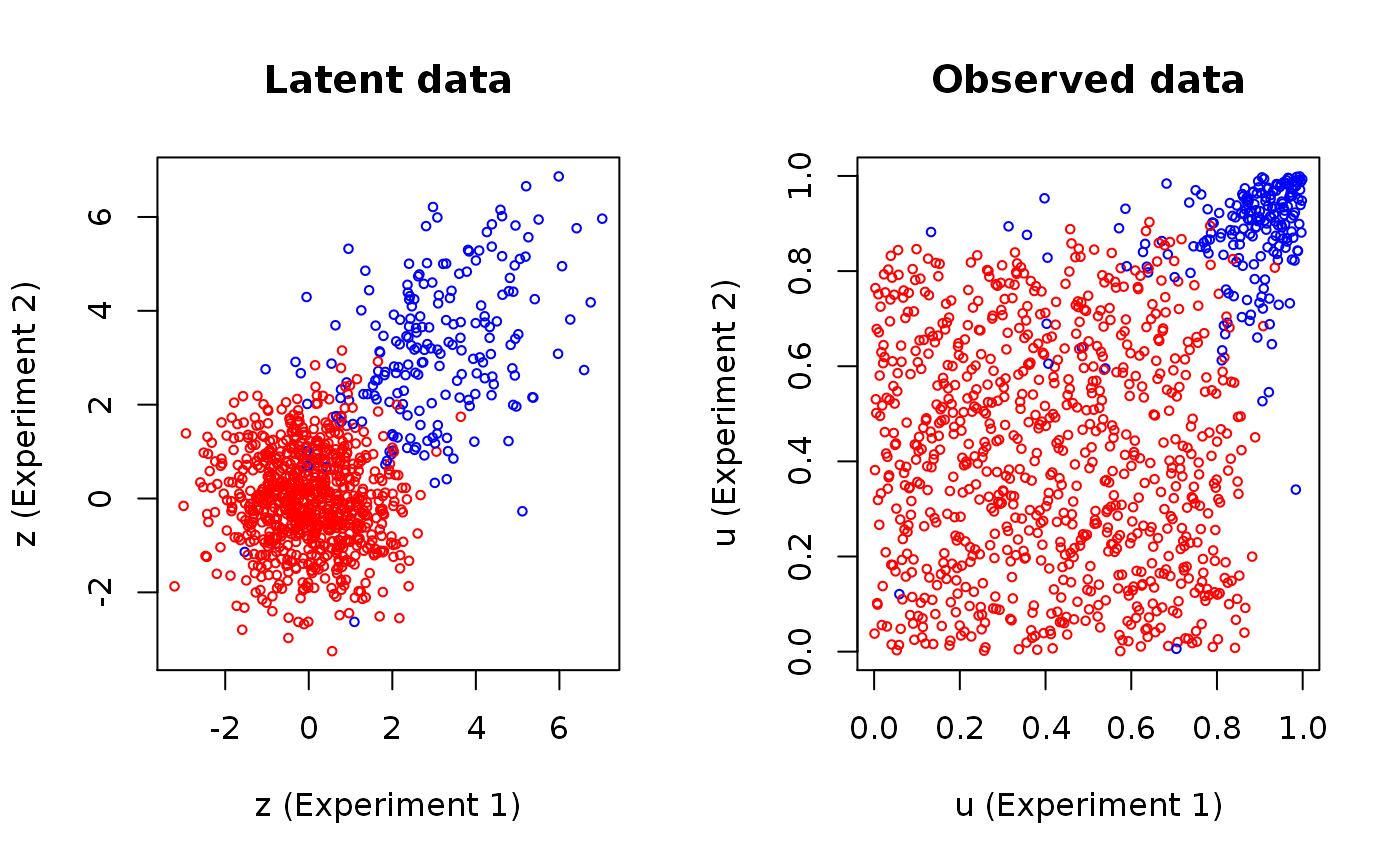
set.seed(1)

# Choosing the true parameters and simulating data
true.par <- c(0.8, 3, 1.5, 0.4)
data <- SimulateGMCMData(n = 1000, par = true.par, d = 2)
uhat <- Uhat(data$u)  # Observed ranks

# Plot of latent and observed data colour coded by the true component
par(mfrow = c(1,2))
plot(data$z, main = "Latent data", cex = 0.6,
     xlab = "z (Experiment 1)", ylab = "z (Experiment 2)",
     col = c("red","blue")[data$K])
plot(uhat, main = "Observed data", cex = 0.6,
     xlab = "u (Experiment 1)", ylab = "u (Experiment 2)",
     col = c("red","blue")[data$K])

# Fit the model using the Pseudo EM algorithm
init.par <- c(0.5, 1, 1, 0.5)
res <- GMCM:::PseudoEMAlgorithm(uhat, meta2full(init.par, d = 2),
                                verbose = TRUE,
                                convergence.criterion = "absGMCM",
                                eps = 1e-4,
                                trace.theta = FALSE,
                                meta.special.case = TRUE)
#> 2 | delta = 17.868577 | gmm = -2885.75 | gmcm =  167.34 
#> 3 | delta = 8.082063 | gmm = -2907.74 | gmcm =  175.42 
#> 4 | delta = 6.050655 | gmm = -2927.31 | gmcm =  181.47 
#> 5 | delta = 5.348391 | gmm = -2945.36 | gmcm =  186.82 
#> 6 | delta = 4.839607 | gmm = -2962.35 | gmcm =  191.66 
#> 7 | delta = 4.347890 | gmm = -2978.45 | gmcm =  196.00 
#> 8 | delta = 3.874041 | gmm = -2993.69 | gmcm =  199.88 
#> 9 | delta = 3.435810 | gmm = -3008.08 | gmcm =  203.31 
#> 10 | delta = 3.052414 | gmm = -3021.64 | gmcm =  206.37 
#> 11 | delta = 2.721477 | gmm = -3034.39 | gmcm =  209.09 
#> 12 | delta = 2.443531 | gmm = -3046.37 | gmcm =  211.53 
#> 13 | delta = 2.211751 | gmm = -3057.62 | gmcm =  213.74 
#> 14 | delta = 2.015994 | gmm = -3068.18 | gmcm =  215.76 
#> 15 | delta = 1.853092 | gmm = -3078.07 | gmcm =  217.61 
#> 16 | delta = 1.715827 | gmm = -3087.35 | gmcm =  219.33 
#> 17 | delta = 1.599870 | gmm = -3096.02 | gmcm =  220.93 
#> 18 | delta = 1.500794 | gmm = -3104.13 | gmcm =  222.43 
#> 19 | delta = 1.416708 | gmm = -3111.69 | gmcm =  223.85 
#> 20 | delta = 1.344361 | gmm = -3118.72 | gmcm =  225.19 
#> 21 | delta = 1.282530 | gmm = -3125.24 | gmcm =  226.47 
#> 22 | delta = 1.228756 | gmm = -3131.26 | gmcm =  227.70 
#> 23 | delta = 1.181350 | gmm = -3136.79 | gmcm =  228.88 
#> 24 | delta = 1.139250 | gmm = -3141.84 | gmcm =  230.02 
#> 25 | delta = 1.100991 | gmm = -3146.39 | gmcm =  231.12 
#> 26 | delta = 1.063712 | gmm = -3150.46 | gmcm =  232.19 
#> 27 | delta = 1.026408 | gmm = -3154.02 | gmcm =  233.21 
#> 28 | delta = 0.987403 | gmm = -3157.07 | gmcm =  234.20 
#> 29 | delta = 0.942761 | gmm = -3159.60 | gmcm =  235.14 
#> 30 | delta = 0.891736 | gmm = -3161.58 | gmcm =  236.04 
#> 31 | delta = 0.831993 | gmm = -3163.02 | gmcm =  236.87 
#> 32 | delta = 0.761030 | gmm = -3163.90 | gmcm =  237.63 
#> 33 | delta = 0.680361 | gmm = -3164.23 | gmcm =  238.31 
#> 34 | delta = 0.590134 | gmm = -3164.02 | gmcm =  238.90 
#> 35 | delta = 0.493854 | gmm = -3163.32 | gmcm =  239.39 
#> 36 | delta = 0.395795 | gmm = -3162.17 | gmcm =  239.79 
#> 37 | delta = 0.301642 | gmm = -3160.62 | gmcm =  240.09 
#> 38 | delta = 0.215391 | gmm = -3158.76 | gmcm =  240.31 
#> 39 | delta = 0.141003 | gmm = -3156.64 | gmcm =  240.45 
#> 40 | delta = 0.079594 | gmm = -3154.35 | gmcm =  240.53 
#> 41 | delta = 0.031830 | gmm = -3151.94 | gmcm =  240.56 
#> 42 | delta = 0.004377 | gmm = -3149.48 | gmcm =  240.55 
#> 43 | delta = 0.030996 | gmm = -3147.00 | gmcm =  240.52 
#> 44 | delta = 0.048803 | gmm = -3144.55 | gmcm =  240.47 
#> 45 | delta = 0.061279 | gmm = -3142.14 | gmcm =  240.41 
#> 46 | delta = 0.069590 | gmm = -3139.79 | gmcm =  240.34 
#> 47 | delta = 0.074513 | gmm = -3137.50 | gmcm =  240.27 
#> 48 | delta = 0.077553 | gmm = -3135.30 | gmcm =  240.19 
#> 49 | delta = 0.079276 | gmm = -3133.16 | gmcm =  240.11 
#> 50 | delta = 0.080348 | gmm = -3131.10 | gmcm =  240.03 
#> 51 | delta = 0.080030 | gmm = -3129.12 | gmcm =  239.95 
#> 52 | delta = 0.079876 | gmm = -3127.20 | gmcm =  239.87 
#> 53 | delta = 0.079019 | gmm = -3125.35 | gmcm =  239.79 
#> 54 | delta = 0.078102 | gmm = -3123.57 | gmcm =  239.71 
#> 55 | delta = 0.077079 | gmm = -3121.84 | gmcm =  239.64 
#> 56 | delta = 0.075983 | gmm = -3120.18 | gmcm =  239.56 
#> 57 | delta = 0.074535 | gmm = -3118.57 | gmcm =  239.49 
#> 58 | delta = 0.072803 | gmm = -3117.02 | gmcm =  239.41 
#> 59 | delta = 0.071558 | gmm = -3115.52 | gmcm =  239.34 
#> 60 | delta = 0.069940 | gmm = -3114.07 | gmcm =  239.27 
#> 61 | delta = 0.068348 | gmm = -3112.66 | gmcm =  239.20 
#> 62 | delta = 0.066729 | gmm = -3111.31 | gmcm =  239.14 
#> 63 | delta = 0.065271 | gmm = -3110.00 | gmcm =  239.07 
#> 64 | delta = 0.063689 | gmm = -3108.74 | gmcm =  239.01 
#> 65 | delta = 0.061805 | gmm = -3107.52 | gmcm =  238.95 
#> 66 | delta = 0.060516 | gmm = -3106.34 | gmcm =  238.89 
#> 67 | delta = 0.058488 | gmm = -3105.20 | gmcm =  238.83 
#> 68 | delta = 0.057113 | gmm = -3104.10 | gmcm =  238.77 
#> 69 | delta = 0.055391 | gmm = -3103.04 | gmcm =  238.72 
#> 70 | delta = 0.053966 | gmm = -3102.01 | gmcm =  238.66 
#> 71 | delta = 0.052288 | gmm = -3101.02 | gmcm =  238.61 
#> 72 | delta = 0.050634 | gmm = -3100.07 | gmcm =  238.56 
#> 73 | delta = 0.049541 | gmm = -3099.15 | gmcm =  238.51 
#> 74 | delta = 0.047722 | gmm = -3098.26 | gmcm =  238.46 
#> 75 | delta = 0.046379 | gmm = -3097.40 | gmcm =  238.41 
#> 76 | delta = 0.044991 | gmm = -3096.57 | gmcm =  238.37 
#> 77 | delta = 0.043599 | gmm = -3095.78 | gmcm =  238.33 
#> 78 | delta = 0.042113 | gmm = -3095.01 | gmcm =  238.28 
#> 79 | delta = 0.040781 | gmm = -3094.27 | gmcm =  238.24 
#> 80 | delta = 0.039585 | gmm = -3093.55 | gmcm =  238.20 
#> 81 | delta = 0.038263 | gmm = -3092.87 | gmcm =  238.17 
#> 82 | delta = 0.037011 | gmm = -3092.20 | gmcm =  238.13 
#> 83 | delta = 0.035897 | gmm = -3091.56 | gmcm =  238.09 
#> 84 | delta = 0.034441 | gmm = -3090.95 | gmcm =  238.06 
#> 85 | delta = 0.033345 | gmm = -3090.36 | gmcm =  238.02 
#> 86 | delta = 0.032295 | gmm = -3089.78 | gmcm =  237.99 
#> 87 | delta = 0.031258 | gmm = -3089.23 | gmcm =  237.96 
#> 88 | delta = 0.030116 | gmm = -3088.71 | gmcm =  237.93 
#> 89 | delta = 0.029077 | gmm = -3088.20 | gmcm =  237.90 
#> 90 | delta = 0.028054 | gmm = -3087.70 | gmcm =  237.87 
#> 91 | delta = 0.027176 | gmm = -3087.23 | gmcm =  237.85 
#> 92 | delta = 0.026403 | gmm = -3086.78 | gmcm =  237.82 
#> 93 | delta = 0.025197 | gmm = -3086.34 | gmcm =  237.80 
#> 94 | delta = 0.024321 | gmm = -3085.92 | gmcm =  237.77 
#> 95 | delta = 0.023404 | gmm = -3085.51 | gmcm =  237.75 
#> 96 | delta = 0.022557 | gmm = -3085.12 | gmcm =  237.72 
#> 97 | delta = 0.021739 | gmm = -3084.75 | gmcm =  237.70 
#> 98 | delta = 0.021174 | gmm = -3084.38 | gmcm =  237.68 
#> 99 | delta = 0.020324 | gmm = -3084.04 | gmcm =  237.66 
#> 100 | delta = 0.019571 | gmm = -3083.70 | gmcm =  237.64 
#> 101 | delta = 0.018864 | gmm = -3083.38 | gmcm =  237.62 
#> 102 | delta = 0.018122 | gmm = -3083.07 | gmcm =  237.60 
#> 103 | delta = 0.017433 | gmm = -3082.78 | gmcm =  237.59 
#> 104 | delta = 0.016851 | gmm = -3082.49 | gmcm =  237.57 
#> 105 | delta = 0.016232 | gmm = -3082.21 | gmcm =  237.55 
#> 106 | delta = 0.015583 | gmm = -3081.95 | gmcm =  237.54 
#> 107 | delta = 0.014975 | gmm = -3081.69 | gmcm =  237.52 
#> 108 | delta = 0.014420 | gmm = -3081.45 | gmcm =  237.51 
#> 109 | delta = 0.013892 | gmm = -3081.22 | gmcm =  237.50 
#> 110 | delta = 0.013395 | gmm = -3080.99 | gmcm =  237.48 
#> 111 | delta = 0.012932 | gmm = -3080.77 | gmcm =  237.47 
#> 112 | delta = 0.012513 | gmm = -3080.56 | gmcm =  237.46 
#> 113 | delta = 0.012074 | gmm = -3080.36 | gmcm =  237.44 
#> 114 | delta = 0.011569 | gmm = -3080.17 | gmcm =  237.43 
#> 115 | delta = 0.011113 | gmm = -3079.98 | gmcm =  237.42 
#> 116 | delta = 0.010670 | gmm = -3079.80 | gmcm =  237.41 
#> 117 | delta = 0.010217 | gmm = -3079.63 | gmcm =  237.40 
#> 118 | delta = 0.009841 | gmm = -3079.47 | gmcm =  237.39 
#> 119 | delta = 0.009477 | gmm = -3079.31 | gmcm =  237.38 
#> 120 | delta = 0.009106 | gmm = -3079.16 | gmcm =  237.37 
#> 121 | delta = 0.008760 | gmm = -3079.01 | gmcm =  237.36 
#> 122 | delta = 0.008448 | gmm = -3078.87 | gmcm =  237.36 
#> 123 | delta = 0.008137 | gmm = -3078.73 | gmcm =  237.35 
#> 124 | delta = 0.007861 | gmm = -3078.60 | gmcm =  237.34 
#> 125 | delta = 0.007550 | gmm = -3078.48 | gmcm =  237.33 
#> 126 | delta = 0.007260 | gmm = -3078.36 | gmcm =  237.32 
#> 127 | delta = 0.007005 | gmm = -3078.24 | gmcm =  237.32 
#> 128 | delta = 0.006747 | gmm = -3078.13 | gmcm =  237.31 
#> 129 | delta = 0.006459 | gmm = -3078.03 | gmcm =  237.30 
#> 130 | delta = 0.006158 | gmm = -3077.92 | gmcm =  237.30 
#> 131 | delta = 0.005900 | gmm = -3077.83 | gmcm =  237.29 
#> 132 | delta = 0.005662 | gmm = -3077.73 | gmcm =  237.29 
#> 133 | delta = 0.005437 | gmm = -3077.64 | gmcm =  237.28 
#> 134 | delta = 0.005224 | gmm = -3077.55 | gmcm =  237.28 
#> 135 | delta = 0.005026 | gmm = -3077.47 | gmcm =  237.27 
#> 136 | delta = 0.004835 | gmm = -3077.39 | gmcm =  237.27 
#> 137 | delta = 0.004638 | gmm = -3077.31 | gmcm =  237.26 
#> 138 | delta = 0.004463 | gmm = -3077.24 | gmcm =  237.26 
#> 139 | delta = 0.004294 | gmm = -3077.17 | gmcm =  237.25 
#> 140 | delta = 0.004129 | gmm = -3077.10 | gmcm =  237.25 
#> 141 | delta = 0.003973 | gmm = -3077.03 | gmcm =  237.24 
#> 142 | delta = 0.003827 | gmm = -3076.97 | gmcm =  237.24 
#> 143 | delta = 0.003688 | gmm = -3076.91 | gmcm =  237.24 
#> 144 | delta = 0.003561 | gmm = -3076.85 | gmcm =  237.23 
#> 145 | delta = 0.003434 | gmm = -3076.79 | gmcm =  237.23 
#> 146 | delta = 0.003304 | gmm = -3076.74 | gmcm =  237.23 
#> 147 | delta = 0.003184 | gmm = -3076.69 | gmcm =  237.22 
#> 148 | delta = 0.003074 | gmm = -3076.64 | gmcm =  237.22 
#> 149 | delta = 0.002949 | gmm = -3076.59 | gmcm =  237.22 
#> 150 | delta = 0.002832 | gmm = -3076.54 | gmcm =  237.21 
#> 151 | delta = 0.002717 | gmm = -3076.50 | gmcm =  237.21 
#> 152 | delta = 0.002608 | gmm = -3076.46 | gmcm =  237.21 
#> 153 | delta = 0.002507 | gmm = -3076.41 | gmcm =  237.21 
#> 154 | delta = 0.002412 | gmm = -3076.38 | gmcm =  237.20 
#> 155 | delta = 0.002342 | gmm = -3076.34 | gmcm =  237.20 
#> 156 | delta = 0.002207 | gmm = -3076.30 | gmcm =  237.20 
#> 157 | delta = 0.002119 | gmm = -3076.27 | gmcm =  237.20 
#> 158 | delta = 0.002034 | gmm = -3076.23 | gmcm =  237.20 
#> 159 | delta = 0.001951 | gmm = -3076.20 | gmcm =  237.19 
#> 160 | delta = 0.001873 | gmm = -3076.17 | gmcm =  237.19 
#> 161 | delta = 0.001798 | gmm = -3076.14 | gmcm =  237.19 
#> 162 | delta = 0.001727 | gmm = -3076.11 | gmcm =  237.19 
#> 163 | delta = 0.001658 | gmm = -3076.08 | gmcm =  237.19 
#> 164 | delta = 0.001592 | gmm = -3076.06 | gmcm =  237.19 
#> 165 | delta = 0.001529 | gmm = -3076.03 | gmcm =  237.18 
#> 166 | delta = 0.001467 | gmm = -3076.01 | gmcm =  237.18 
#> 167 | delta = 0.001409 | gmm = -3075.99 | gmcm =  237.18 
#> 168 | delta = 0.001353 | gmm = -3075.96 | gmcm =  237.18 
#> 169 | delta = 0.001299 | gmm = -3075.94 | gmcm =  237.18 
#> 170 | delta = 0.001248 | gmm = -3075.92 | gmcm =  237.18 
#> 171 | delta = 0.001199 | gmm = -3075.90 | gmcm =  237.18 
#> 172 | delta = 0.001152 | gmm = -3075.88 | gmcm =  237.17 
#> 173 | delta = 0.001107 | gmm = -3075.86 | gmcm =  237.17 
#> 174 | delta = 0.001063 | gmm = -3075.85 | gmcm =  237.17 
#> 175 | delta = 0.001021 | gmm = -3075.83 | gmcm =  237.17 
#> 176 | delta = 0.000980 | gmm = -3075.81 | gmcm =  237.17 
#> 177 | delta = 0.000942 | gmm = -3075.80 | gmcm =  237.17 
#> 178 | delta = 0.000904 | gmm = -3075.78 | gmcm =  237.17 
#> 179 | delta = 0.000869 | gmm = -3075.77 | gmcm =  237.17 
#> 180 | delta = 0.000834 | gmm = -3075.76 | gmcm =  237.17 
#> 181 | delta = 0.000802 | gmm = -3075.74 | gmcm =  237.17 
#> 182 | delta = 0.000771 | gmm = -3075.73 | gmcm =  237.17 
#> 183 | delta = 0.000741 | gmm = -3075.72 | gmcm =  237.16 
#> 184 | delta = 0.000712 | gmm = -3075.71 | gmcm =  237.16 
#> 185 | delta = 0.000684 | gmm = -3075.70 | gmcm =  237.16 
#> 186 | delta = 0.000657 | gmm = -3075.68 | gmcm =  237.16 
#> 187 | delta = 0.000633 | gmm = -3075.67 | gmcm =  237.16 
#> 188 | delta = 0.000608 | gmm = -3075.66 | gmcm =  237.16 
#> 189 | delta = 0.000585 | gmm = -3075.65 | gmcm =  237.16 
#> 190 | delta = 0.000562 | gmm = -3075.65 | gmcm =  237.16 
#> 191 | delta = 0.000540 | gmm = -3075.64 | gmcm =  237.16 
#> 192 | delta = 0.000520 | gmm = -3075.63 | gmcm =  237.16 
#> 193 | delta = 0.000499 | gmm = -3075.62 | gmcm =  237.16 
#> 194 | delta = 0.000480 | gmm = -3075.61 | gmcm =  237.16 
#> 195 | delta = 0.000462 | gmm = -3075.60 | gmcm =  237.16 
#> 196 | delta = 0.000444 | gmm = -3075.60 | gmcm =  237.16 
#> 197 | delta = 0.000427 | gmm = -3075.59 | gmcm =  237.16 
#> 198 | delta = 0.000411 | gmm = -3075.58 | gmcm =  237.16 
#> 199 | delta = 0.000395 | gmm = -3075.58 | gmcm =  237.16 
#> 200 | delta = 0.000380 | gmm = -3075.57 | gmcm =  237.16 
#> 201 | delta = 0.000365 | gmm = -3075.57 | gmcm =  237.16 
#> 202 | delta = 0.000351 | gmm = -3075.56 | gmcm =  237.15 
#> 203 | delta = 0.000337 | gmm = -3075.55 | gmcm =  237.15 
#> 204 | delta = 0.000324 | gmm = -3075.55 | gmcm =  237.15 
#> 205 | delta = 0.000312 | gmm = -3075.54 | gmcm =  237.15 
#> 206 | delta = 0.000300 | gmm = -3075.54 | gmcm =  237.15 
#> 207 | delta = 0.000288 | gmm = -3075.53 | gmcm =  237.15 
#> 208 | delta = 0.000277 | gmm = -3075.53 | gmcm =  237.15 
#> 209 | delta = 0.000266 | gmm = -3075.53 | gmcm =  237.15 
#> 210 | delta = 0.000256 | gmm = -3075.52 | gmcm =  237.15 
#> 211 | delta = 0.000246 | gmm = -3075.52 | gmcm =  237.15 
#> 212 | delta = 0.000236 | gmm = -3075.51 | gmcm =  237.15 
#> 213 | delta = 0.000227 | gmm = -3075.51 | gmcm =  237.15 
#> 214 | delta = 0.000218 | gmm = -3075.51 | gmcm =  237.15 
#> 215 | delta = 0.000210 | gmm = -3075.50 | gmcm =  237.15 
#> 216 | delta = 0.000202 | gmm = -3075.50 | gmcm =  237.15 
#> 217 | delta = 0.000194 | gmm = -3075.50 | gmcm =  237.15 
#> 218 | delta = 0.000186 | gmm = -3075.49 | gmcm =  237.15 
#> 219 | delta = 0.000179 | gmm = -3075.49 | gmcm =  237.15 
#> 220 | delta = 0.000172 | gmm = -3075.49 | gmcm =  237.15 
#> 221 | delta = 0.000165 | gmm = -3075.48 | gmcm =  237.15 
#> 222 | delta = 0.000159 | gmm = -3075.48 | gmcm =  237.15 
#> 223 | delta = 0.000153 | gmm = -3075.48 | gmcm =  237.15 
#> 224 | delta = 0.000147 | gmm = -3075.48 | gmcm =  237.15 
#> 225 | delta = 0.000141 | gmm = -3075.48 | gmcm =  237.15 
#> 226 | delta = 0.000135 | gmm = -3075.47 | gmcm =  237.15 
#> 227 | delta = 0.000130 | gmm = -3075.47 | gmcm =  237.15 
#> 228 | delta = 0.000125 | gmm = -3075.47 | gmcm =  237.15 
#> 229 | delta = 0.000120 | gmm = -3075.47 | gmcm =  237.15 
#> 230 | delta = 0.000116 | gmm = -3075.46 | gmcm =  237.15 
#> 231 | delta = 0.000111 | gmm = -3075.46 | gmcm =  237.15 
#> 232 | delta = 0.000107 | gmm = -3075.46 | gmcm =  237.15 
#> 233 | delta = 0.000103 | gmm = -3075.46 | gmcm =  237.15 
#> 234 | delta = 0.000099 | gmm = -3075.46 | gmcm =  237.15 

# Compute posterior cluster probabilities
IDRs <- get.IDR(uhat, par = full2meta(res$theta))

# Plot of observed data colour coded by the MAP estimate
plot(res$loglik[3,], main = "Loglikelihood trace", type = "l",
     ylab = "log GMCM likelihood")
abline(v = which.max(res$loglik[3,])) # Chosen MLE
plot(uhat, main = "Clustering\nIDR < 0.05", xlab = "", ylab = "", cex = 0.6,
     col = c("Red","Blue")[IDRs$Khat])

# View parameters
rbind(init.par, true.par, estimate = full2meta(res$theta))
#>               pie1    mu.mu     sigma       rho
#> init.par 0.5000000 1.000000 1.0000000 0.5000000
#> true.par 0.8000000 3.000000 1.5000000 0.4000000
#> estimate 0.8224538 2.521749 0.8548858 0.4069159

# Confusion matrix
table("Khat" = IDRs$Khat, "K" = data$K)
#>     K
#> Khat   1   2
#>    1 797  37
#>    2   5 161