EM algorithm for Gaussian mixture models

The regular expectation-maximization algorithm for general multivariate Gaussian mixture models.

EMAlgorithm(x, theta, m, eps = 1e-06, max.ite = 1e+05,
  trace.theta = FALSE, verbose = FALSE)

Arguments

x	A `matrix` of observations where each row correspond to an observation and each columns to a feature/variable.
theta	A list of parameters of class `theta` as described in `rtheta`. Optional. If not provided `m` should be given.
m	`numeric`. The number of components if `theta` is not supplied.
eps	The maximal required difference in successive likelihoods to establish convergence.
max.ite	The maximum number of iterations.
trace.theta	Logical. If `TRUE`, all estimates are stored and returned. Default is `FALSE`.
verbose	Set to `TRUE` for verbose output. Default is `FALSE`.

Value

A list of length 3 with elements:

theta

A list of the estimated parameters as described in rtheta.

loglik.tr

A numeric vector of the log-likelihood trace.

kappa

A matrix where kappa[i,j] is the probability that x[i, ] is realized from the j'th component.

Details

Though not as versatile, the algorithm can be a faster alternative to Mclust in the mclust-package. If theta is not given, a k-means clustering is used to determine the initial theta.

Author

Anders Ellern Bilgrau <anders.ellern.bilgrau@gmail.com>

Examples

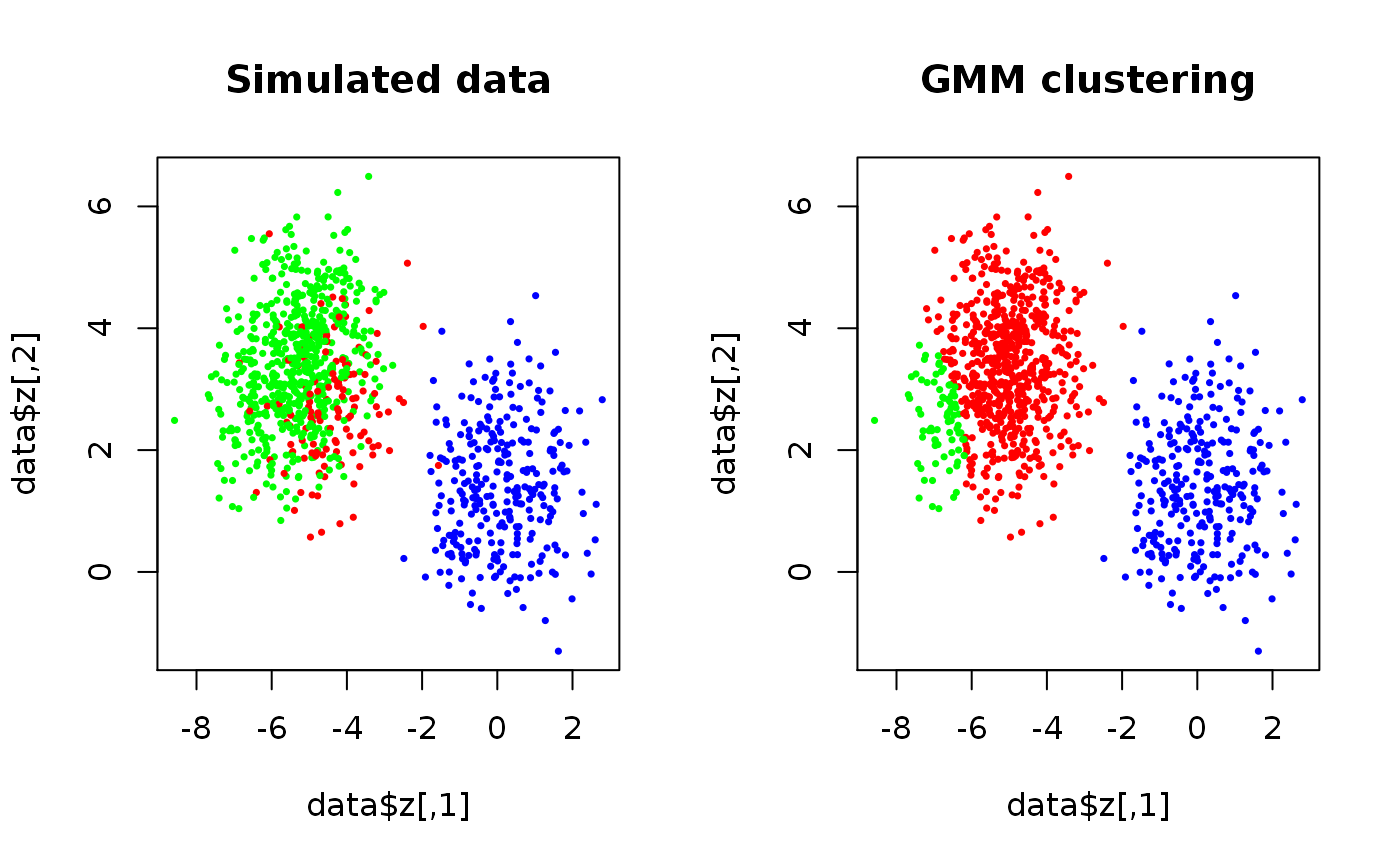
set.seed(3)
true.theta <- rtheta(d = 2, m = 3, method = "old")
true.theta$sigma <- lapply(true.theta$sigma, cov2cor) # Scale
if (FALSE) {
plot(true.theta, nlevels = 20, add.ellipses = TRUE)
}

data <- SimulateGMCMData(n = 1000, theta = true.theta)
start.theta <- rtheta(d = 2, m = 3)
start.theta$mu <- t(kmeans(data$z, 3)$centers) # More sensible location estimates
start.theta <- as.theta(start.theta) # Coerce the matrix to a list
res <- GMCM:::EMAlgorithm(data$z, theta = start.theta)

par(mfrow = c(1,2))
plot(data$z, cex = 0.5, pch = 16, main = "Simulated data",
     col = rainbow(3)[data$K])
plot(data$z, cex = 0.5, pch = 16, main = "GMM clustering",
     col = rainbow(3)[apply(res$kappa,1,which.max)])